Hudson-Kreitman-Aquadé test

---

When dealing with polymorphisms from non-coding regions from multiple loci (or a mixture of coding and non-coding regions), Hudson-Kreitman-Aquadé (1987) test can be used.

Consider two closely related species. Suppose DNA samples were taken from each species at m loci. For locus i, there are three quantities that are readily found from the samples:

• K_ij - number of segregating sites in the sample from species j (j = 1, 2)
• D_i - average number of nucleotide differences between two sequences, one from each sample.

if one can compute the mean and variance of K_ij and D_i under a null hypothesis, a goodness of fit statistic can be constructed to test the null hypothesis. The test using the statistics

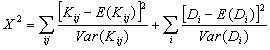is known as the Hudson-Kreitman-Aquadé (HKA) test. Each term in X² is the square of a normalized variable whose mean and variance are approximately 0 and 1 respectively. As long as these normalized variables roughly follow the standard normal distribution, X² will have an approximate Chi-square distribution. Simulations shows that the distribution of X² is indeed close to Chi-square distribution with (2m-2) df. The reason for (2m-2) degree of freedom rather than 3m is that (m+2) parameters have to be estimated.

In order for HKA test to have non-zero degree of freedom, it is necessary that data from at least two loci are available. Also for (2m-2) to be the correct degree of freedom, it is important that loci being studied are unlinked or in linkage equilibrium. It should be noted that HKA test implicitly assumes that the divergence time T is large enough so that the common ancestral sequence of the samples is younger than T. It is also assumed the effective population sizes are the same for all loci, which implies that is is not appropriate to combine data from nuclear, sex-chromosome and mitochondria.